Cưc đại và cực tiểu là gì? Cách xác định điểm cực trị của hàm số
Định nghĩa điểm cực đại cực tiểu
Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên khoảng $\left( a;b \right)$ (có thể $a$ là $-\infty $; $b$ là $+\infty $) và điểm ${{x}_{0}}\in \left( a;b \right)$
a) Nếu tồn tại số $h>0$ sao cho $f\left( x \right)<f\left( {{x}_{0}} \right)$ với mọi $x\in \left( {{x}_{0}}-h;{{x}_{0}}+h \right)$ và $x\ne {{x}_{0}}$ thì ta nói hàm số $f\left( x \right)$ đạt cực đại tại ${{x}_{0}}$.
b) Nếu tồn tại số $h>0$ sao cho $f\left( x \right)>f\left( {{x}_{0}} \right)$ với mọi $x\in \left( {{x}_{0}}-h;{{x}_{0}}+h \right)$ và $x\ne {{x}_{0}}$ thì ta nói hàm số $f\left( x \right)$ đạt cực tiểu tại ${{x}_{0}}$.
Chú ý về điểm cực trị
- Nếu hàm số $f\left( x \right)$đạt cực đại (cực tiểu) tại điểm ${{x}_{0}}$ thì ${{x}_{0}}$được gọi là điểm cực đại (điểm cực tiểu) của hàm số; $f\left( {{x}_{0}} \right)$ được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, ký hiệu là ${{f}_{CD}}\left( {{f}_{CT}} \right)$, còn điểm $M\left( {{x}_{0}};f\left( {{x}_{0}} \right) \right)$ được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
- Các điểm cực đại cực tiểu được gọi chung là điểm cực trị.
- Dễ dàng chứng minh được rằng, nếu hàm số $y=f\left( x \right)$ có đạo hàm trên khoảng $\left( a;b \right)$ và đạt cực đại hoặc cực tiểu tại ${{x}_{0}}$ thì $f'\left( {{x}_{0}} \right)=0.$
Định lý 1: Giả sử hàm số $y=f\left( x \right)$liên tục trên khoảng $K=\left( {{x}_{0}}-h;{{x}_{0}}+h \right)$ và có đạo hàm trên $K$ hoặc trên $K\backslash \left\{ {{x}_{0}} \right\},$ với $h>0$.
- Nếu $f'\left( {{x}_{0}} \right)>0$ trên khoảng $\left( {{x}_{0}}-h;{{x}_{0}} \right)$và $f'\left( {{x}_{0}} \right)<0$ trên khoảng $\left( {{x}_{0}};{{x}_{0}}+h \right)$ thì ${{x}_{0}}$ là điểm cực đại của hàm số $f\left( x \right).$
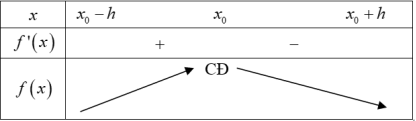
- Nếu $f'\left( {{x}_{0}} \right)<0$ trên khoảng $\left( {{x}_{0}}-h;{{x}_{0}} \right)$và $f'\left( {{x}_{0}} \right)>0$ trên khoảng $\left( {{x}_{0}};{{x}_{0}}+h \right)$ thì ${{x}_{0}}$ là điểm cực tiểu của hàm số $f\left( x \right).$
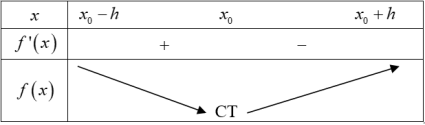
Nhận xét: Xét hàm số $y=f\left( x \right)$ liên tục và xác định trên $\left( a;b \right)$ và ${{x}_{0}}\in \left( a;b \right).$
- Nếu $f'\left( x \right)$ đổi dấu khi qua điểm ${{x}_{0}}$ thì ${{x}_{0}}$ là điểm cực trị của hàm số.
- Nếu $f'\left( x \right)$ đổi dấu từ dương sang âm khi qua điểm ${{x}_{0}}$ thì ${{x}_{0}}$ là điểm cực đại của hàm số.
- Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương khi qua điểm ${{x}_{0}}$ thì ${{x}_{0}}$ là điểm cực tiểu của hàm số.
Chú ý: Hàm số $y=\sqrt{{{x}^{2}}}=\left| x \right|$ có đạo hàm là $y'=\frac{2x}{2\sqrt{{{x}^{2}}}}$ không có đạo hàm tại điểm $x=0$ tuy nhiên $y'$ vẫn đổi dấu từ âm sang dương khi qua điểm $x=0$ nên hàm số đạt cực tiểu tại điểm $x=0$.
Định lý 2: Giả sử hàm số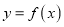 
có đạo hàm cấp hai trong khoảng 
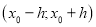với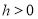 
. Khi đó:
- Nếu $\left\{ \begin{matrix} f'\left( {{x}_{0}} \right)=0 \\ f''\left( {{x}_{0}} \right)>0 \\\end{matrix} \right.\Rightarrow {{x}_{0}}$ là điểm cực tiểu.
- Nếu $\left\{ \begin{matrix} f'\left( {{x}_{0}} \right)=0 \\ f''\left( {{x}_{0}} \right)<0 \\\end{matrix} \right.\Rightarrow {{x}_{0}}$ là điểm cực đại.
Chú ý: Nếu $f'\left( {{x}_{0}} \right)=0$ và $f''\left( {{x}_{0}} \right)=0$ thì chưa thể khẳng định được ${{x}_{0}}$ là điểm cực đại hay điểm cực tiểu hay cực trị của hàm số.
Bài tập: Hàm số $y={{x}^{3}}$ có $\left\{ \begin{matrix} f'\left( 0 \right)=0 \\ f''\left( 0 \right)=0 \\\end{matrix} \right.$ tuy nhiên hàm số này không đạt cực trị tại điểm $x=0$.
Hàm số $y={{x}^{4}}$ có $\left\{ \begin{matrix} f'\left( 0 \right)=0 \\ f''\left( 0 \right)=0 \\\end{matrix} \right.$ tuy nhiên hàm số này đạt cực tiểu tại điểm 
.
Do vậy ta chú ý định lý 2 chỉ đúng theo một chiều (không có chiều ngược lại).